
Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, This is easy to remember if you think about the base as the bottom of an object and the denominator as the bottom of a fraction.Want to cite, share, or modify this book? This book uses the The argument a of the denominator becomes the new base, and the argument x of the numerator becomes the new argument. X Research source One log divided by another, both with the same base b, is equal to a single log. This property holds true because any number with an exponent of zero is equal to one. If the argument is one the answer is always zero. How many times should one multiply a by itself to get a? Once. This is very easy to remember if one thinks about the logarithm in exponential form. If the base a equals the argument a the answer is 1. Basically this is another version of the previous property. If the argument x of the log has an exponent r, the exponent can be moved to the front of the logarithm. (This also works in reverse.)Ī log of two numbers being divided by each other, x and y, can be split into two logs: the log of the dividend x minus the log of the divisor y. X Research sourceĪ log of two numbers, x and y, that are being multiplied by each other can be split into two separate logs: a log of each of the factors being added together. These properties are for use when solving equations. The properties of logarithms are listed below with a separate example for each one with numbers instead of variables. X Research source These only work if the base a and the argument are positive. The properties of logarithms allow you to solve logarithmic and exponential equations that would be otherwise impossible.
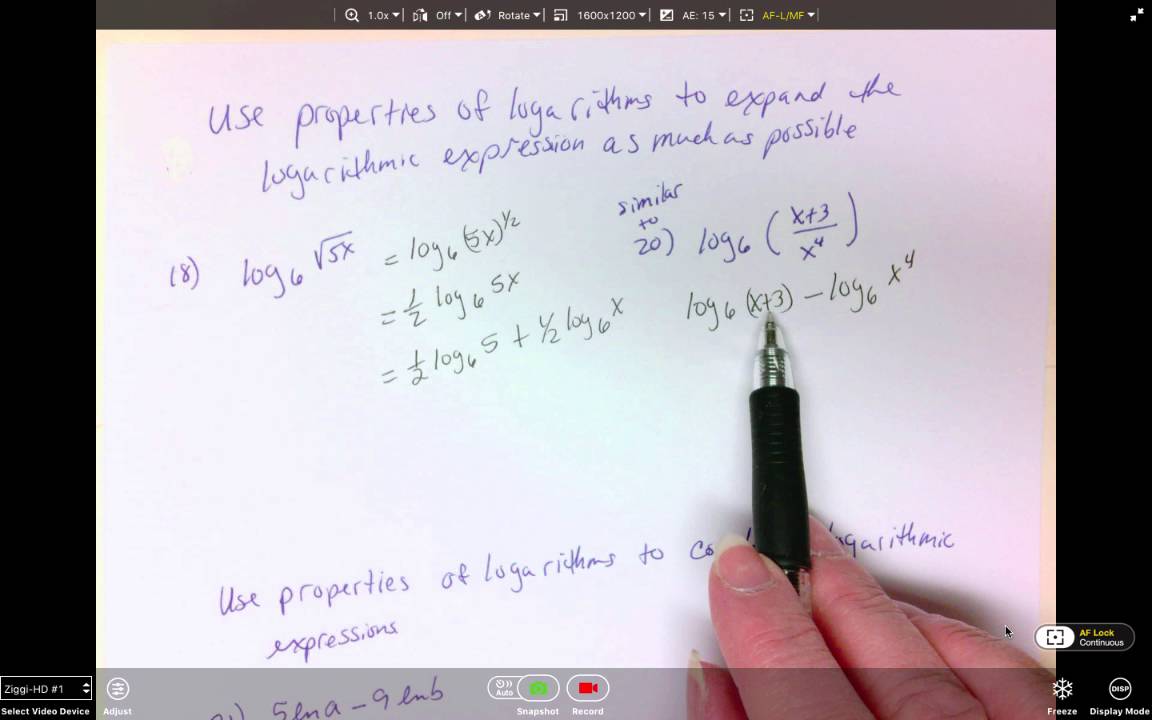
Know and apply the properties of logarithms. To expand a logarithm or to condense a log expression into one logarithm, use the appropriate log rules. Logs that have the 64 th base are used in Advanced Computer Geometry ( ACG) domain. These printable expanding and condensing logarithms worksheets are answered with a lot of get-up-and-go.
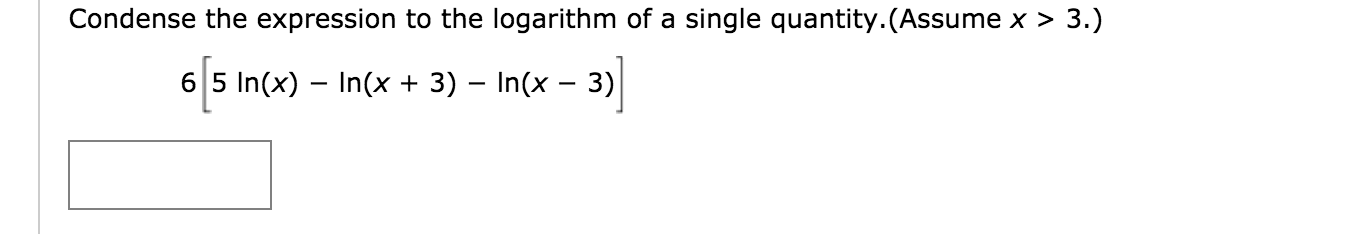
Binary logs have a base of 2 (for the example, log 2x).


In other words, it's an irrational number that we round to 2.71828. You can think of it like the value of pi where there is an infinite number of digits after the decimal place. It's important to understand that 2.71828 or e is not an exact value. The larger the value we plug in for n, the closer we get to 2.71828. e is a mathematical constant that is equal to the limit of (1 + 1/n) n as n approaches infinity, which is approximately equal to 2.718281828. Condense logarithmic expressions Start by applying Rule 2 (Power Rule) in reverse to take care of the constants or numbers on the left of the logs. Natural logs: These are logs with a base of e.Math is a subject that can be difficult for many students. If a log is written without a base (as log x), then it is assumed to have a base of 10. log(5) + log(2) log ( 5) + log ( 2) Use the product property of logarithms, logb(x)+ logb(y) logb(xy) log b ( x) + log b ( y) log b ( x y). Know the difference between a common log and a natural log.


 0 kommentar(er)
0 kommentar(er)
